What is mRNA?
mRNA is made up of four nucleotide bases: adenine (A), cytosine (C), guanine (G), and uracil (U).
What is protein?
Protein is made up of 20 types of amino acids, which are linked together in a linear sequence to form long chains. These chains fold into specific three-dimensional shapes that determines protein's function.
What is the relationship between mRNA and protein?
mRNA serves as a template for synthesizing proteins by assembling amino acids in a specific order. This procedure is called translation. A set of three nucleotide bases, such as AUA, UCU, called codons, specific a particular amino acid.
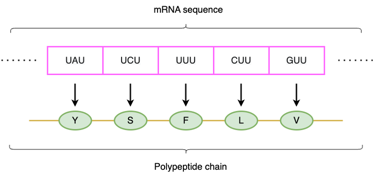
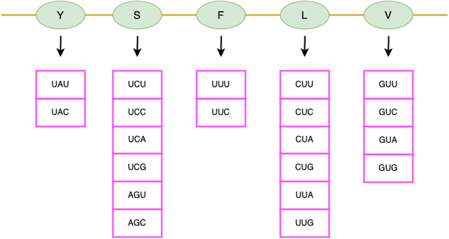
Synonymous codons
A codon has three nucleotides. Three nucleotides can have 64 possible codons (4 ^ 3 = 64), however, there are only 20 types of amino acids. So some codons that can encode the same amino acid is called Synonymous codons.
The table above shows a clearer mapping between amino acids and their corresponding mRNA codons.
| Amino Acid | mRNA Codons | Amino Acid | mRNA Codons |
|---|---|---|---|
| Ala (A) | GCU, GCC, GCA, GCG | Ile (I) | AUU, AUC, AUA |
| Arg (R) | CGU, CGC, CGG, AGA, ACG | Leu (L) | CUU, CUC, CUA, CUG, UUA, UUC |
| Asn (N) | AAU, AAC | Lys (K) | AAA, AAG |
| Asp (D) | GAU, GAC | Met (M) | AUG |
| Asn or Asp (B) | AAU, AAC, GAU, GAC | Rhe (F) | UUU, UUC |
| Cys (C) | UGU, UGC | Pro (P) | CCU, CCC, CCA, CCG |
| Gln (Q) | CAA, CAG | Ser (S) | UCU, UCC, UCA, UCG, AGU, AGC |
| Glu (E) | GAA, GAG | Thr (T) | ACU, ACC, ACA, ACG |
| Gln or Glu (Z) | CAA, CAG, GAA, GAG | Trp (W) | UGG |
| Gly (G) | GGU, GGC, GGA, GGG | Tyr (Y) | UAU, UAC |
| His (H) | CAU, CAC | Val (V) | GUU, GUC, GUA, GUG |
| START | AUG, CUG, UUG | STOP | UAA, UGA, UAG |
Table: Amino Acids and Their mRNA Codon Mappings
What is mRNA codon optimization?
In mRNA vaccine development, when designing an mRNA sequence to produce a specific protein (or antigen) in host cells, it's important to consider the fact that each amino acid in the protein sequence can be encoded by multiple possible mRNA codons.
mRNA codon optimization refers to the process of selecting the best mRNA codons for encoding a specific amino acid sequence in order to enhance protein expression and stability. In mRNA vaccine development, this step is essential for ensuring that mRNA vaccine produces the target protein effectively.
This is a Combinatorial Optimization Problem because for each amino acid, there are multiple synonymous codons that encode the same amino acid. This results in a large number of possible codon sequences for a given protein. The solution space grows exponentially, with the total number of possible codon combinations being 6^N, where N is the length of the protein. This is because, in the worst case, each amino acid can be encoded by up to 6 different codons. As the protein length increases, the number of possible codon sequences expands exponentially, creating a vast search space that must be explored to find the optimal solution.
Quantum Computing Approach for mRNA codon optimization
Quantum computing offers significant potential advantages over classical computing, especially in solving complex problems that involve large amounts of data, intricate computations, or combinatorial optimization.
I have developed a quantum computing-based method for mRNA codon optimization, addressing the combinatorial complexity of selecting optimal codons for protein expression. This approach leverages the unique advantages of quantum computing to efficiently navigate the vast solution space of synonymous codon combinations.
Here is the quantum computing procedure for mRNA codon optimization as illustrated in the figure.
Step 1. Encode codons to Qubits
When applying quantum computing, classical data is encoded into qubits for processing. There are typically two kinds of encoding: one-hot and dense encoding.
One-hot encoding: each synonymous codon for an amino acid is represented by a binary vector, where only one position in the vector is ”1” (indicating the selected codon), and other positions are “0”. For example, amino acid Ala (A) and Leu (L) are encoded by one-hot method at the following tables.
| Synonymous Codons of Leu | One-Hot Encoding |
|---|---|
| CUU | 100000 |
| CUC | 010000 |
| CUA | 001000 |
| CUG | 000100 |
| UUA | 000010 |
| UUG | 000001 |
Table 1 Leu (L) is encoded by one-hot method
| Synonymous Codons of Ala (A) | Dense Encoding |
|---|---|
| GCU | 1000 |
| GCC | 0100 |
| GCA | 0010 |
| GCG | 0001 |
Table 2 Ala (A) is encoded by one-hot method
Note: Redundant string of Leu (L) or Ala (A): Have all “0” or multiple ”1”. For example, 110110 for Leu is a redundant string, and 1110 for Ala is also a redundant string.
The required number of qubits for a protein with the length of N:
\[S_{one-hot} = \sum_{i=0}^{N-1} C_{i}\]
Where \(C_i\) represents the number of synonymous codons for the i-th amino acid in a protein.
Dense encoding: apply a logarithmic mapping to represent synonymous codons. Amino acid Ala (A) and Leu (L) are still as examples at the following table.
| Synonymous Codons of Leu (L) | Dense Encoding |
|---|---|
| CUU | 000 |
| CUC | 001 |
| CUA | 010 |
| CUG | 011 |
| UUA | 100 |
| UUG | 101 |
Table 3 Leu (L) is encoded by dense method
| Synonymous Codons of Ala (A) | Dense Encoding |
|---|---|
| GCU | 00 |
| GCC | 01 |
| GCA | 10 |
| GCG | 11 |
Table 4 Ala (A) is encoded by dense method
Note: In the dense encoding, 110 and 111 for Leu are redundant strings, and Ala has no redundant string.
The required number of qubits for a protein with the length of N:
\[S_{dense} = \sum_{i=0}^{N-1} \lceil \text{log }C_{i} \rceil\]
Where \(C_{i}\) represents the number of synonymous codons for the i-th amino acid in a protein.
| Encoding method | Qubits required | Pros | Cons |
|---|---|---|---|
| One-Hot | O(N) | Clear representation and simple for the energy function | Resource-intensive for large data |
| Dense | Log(N) | Efficient resource | Complex for the energy fucntion |
Table 5 Comparison between one-hot and dense encoding
Dense encoding was used for mRNA codon optimization because it used fewer qubits than one-hot, making it more scalable and efficient for quantum computing.
Step 2. Construct the energy function
The target of mRNA codon optimization is to select the optimal mRNA sequences that can efficiently translate to a specific protein. This process takes into account several factors, including usage bias, GC target content, and the avoidance of consecutive repeats.
- Usage bias: it refers to the preference of certain synonymous codons over others for encoding the same amino acid. Optimizing codon usage ensures that the mRNA sequence aligns with the host organism's translation, enhancing protein expression and stability.
- GC target content: it refers to the percentage of G and C nucleotides among the mRNA sequence in different organism. Deviating too far from the target GC content can impact mRNA translation efficiency.
- Avoiding repeats: consecutive nucleotide repeats can lead to ribosomal stall, translation errors, and unwanted secondary structure of mRNA. Minimizing repeats can achieve higher protein production.
- Penalty: redundant strings are penalized because these codons can not translate correct amino acids.
\[H(q) = H_{f}(q) + H_{gc}(q) + H_{r}(q) + H_{p}(q)\]
Where \(H_{f}\)(q) represents codon usage bias, \(H_{gc}\)(q) represents target GC concentration, \(H_r\)(q) for sequentially repeated nucleotides, \(H_p\)(q) for constraint items related to redundant encoding.
The paper [1] introduced how to construct the energy function in detail for mRNA codon optimization through dense encoding.
Step 3. Run VQE
After constructing the energy function, VQE was executed on Quantum simulators for finding the optimal mRNA sequence.
- Dataset: 160 sequences, each has 8 amino acids
- Platform: quantum simulator
- VQE library: SamplingVQE
- Ansatz : EfficientSU2
- Hamiltonian: From the energy function
- Optimization: COBYLA
Step 4. Decode to mRNA sequences
The result from the Variational Quantum Eigensolver (VQE) is a qubit string, which must be decoded into the corresponding mRNA sequence. This decoded sequence is the final outcome of the mRNA codon optimization process. The final mRNA sequence represents the optimal codon choices that will efficiently translate into the target protein. This optimized sequence is designed to ensure maximum protein expression, stability, and translation efficiency in the host cells, considering factors like codon usage bias, GC content, and avoiding repeats.
Results from a simple example:- Input Amino Acid Sequence: HAIHVSGT
- The required number of qubit: 15
- Minimal Value Achieved: 3937.05
- Final String Representation: 110001100000101
- Optimal mRNA Codon Sequence: CAU GCG AUA CAU GUG AGC GGC ACC
Optimized Codon Mapping:H → 1 → CAU
A → 10 → GCG
I → 00 → AUA
H → 1 → CAU
V → 10 → GUG
S → 000 → AGC
G → 01 → GGC
T → 01 → ACC
Conclusion
In conclusion, mRNA codon optimization is a crucial step in mRNA vaccine development and protein expression. By leveraging quantum computing techniques, particularly the Variational Quantum Eigensolver (VQE), we can efficiently explore the vast solution space of codon combinations. The quantum approach allows for the optimization of mRNA sequences by selecting the most suitable codons, considering factors such as codon usage bias, GC content, and avoiding repeated patterns. The final outcome is an optimized mRNA sequence, capable of effectively translating into the desired protein, thereby enhancing protein expression and stability in host cells. This innovative method opens up new possibilities for improving the efficiency of mRNA vaccines and other biotechnological applications, demonstrating the potential of quantum computing in solving complex biological problems.
While the method demonstrates the potential of quantum computing for mRNA codon optimization, it is currently limited by the finite number of qubits available on quantum computers. As a result, it may not be feasible to solve protein sequences of large-scale real-world length at this stage. However, this approach serves as a proof of concept, showcasing that quantum computing can be applied to the optimization of mRNA codons. As quantum hardware continues to evolve, it is expected that the scalability of these methods will improve, enabling them to tackle more complex biological problems and larger protein sequences in the future.
Reference
1. Zhang, H., Sarkar, A., & Bertels, K. (2024). A resource-efficient variational quantum algorithm for mRNA codon optimization. arXiv preprint arXiv:2404.14858.
2. Dillion M Fox, Kim M Branson, and Ross C Walker. mrna codon optimization with quantum computers. PloS one, 16(10):e0259101, 2021.