Protein Folding

What is protein folding?

Protein folding is the physical process by which a polypeptide chain produces a three-dimensional structure. It involves primary structure, secondary structure, tertiary structure, and quaternary structure. The structure of a protein is crucial for its functions, as it determines how the protein interacts with other molecules in the cell.

The four levels of protein structure

1. Primary structure: The linear sequence of amino acids join together, which is determined by the genetic code in DNA.

2. Secondary structure: The structures, such as alpha helices and beta sheets, are stabilized by hydrogen bonding between the backbone atoms of amino acids.

3. Tertiary structure: It arises from the folding of secondary structure elements and interactions between amino acids.

4. Quaternary structure: Multiple proteins fold into a larger and functional protein.

How to use quantum computing algorithm to predict tertiary structure of a protein?

Here, I explore the utilization of quantum algorithms for protein folding into tertiary structures. Protein folding involves predicting the three-dimensional structure of a protein from its amino acid sequence, with the goal of finding the conformation with the minimum energy. To address this challenge, I employ Variational Quantum Eigensolver (VQE) that can efficiently approximate the ground state energy of quantum systems. By leveraging VQE, I aim to advance our understanding of protein folding and contribute to the development of novel computational approaches in structural biology.

Due to the limited number of qubits available on current quantum computers, executing quantum protein folding becomes challenging for longer amino acid sequences. This limitation constrains the size and complexity of the protein structures that can be accurately modeled with quantum algorithms. As a result, while quantum computing holds promise for advancing protein folding research, overcoming hardware constrains remains a critical challenge that requires further exploration and innovation.

Simplifying protein folding on a diamond lattice provides a foundational framework to illustrate quantum approaches for studying protein folding. In this simplified model, proteins are represented as linear chains of amino acids arranged on a lattice resembling the crystalline structure of diamond. Each amino acid is positioned at a lattice site, and the connections between them mimic the bonds in the protein backbone. Importantly, the angle and distance of amino acids are constrained by the lattice structure, reflecting the geometric limitations imposed by the lattice geometric. It can be allowed to investigate quantum approaches for protein folding processes.

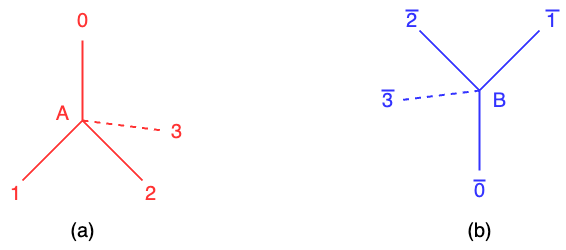
The quantum method described in the reference [1] encodes the directions of two adjacent amino acids on a lattice model as turns, which involves the relative orientation or angular displacement between the amino acids. In the simplified diamond model, the connections between lattice sites represent the bonds between adjacent amino acids in the protein chain. All of amino acids are positioned at either the sub-lattice A or B in the Figure 1 (a) and (b). Each sub-lattice contains beads representing and these beads have four turns: {0, 1, 2, 3} at the sub-lattice A or {\(\overline{0}, \overline{1}, \overline{2}, \overline{3}\)} at the sub-lattice B. These turns correspond to the relative orientations of the amino acids and define the angular displacement between them. Each lattice site or bead in the lattice structure is assigned to either sub-lattice A or B in an alternating manner. This arrangement ensures that the lattice structure maintains its periodicity and symmetry. Therefore, in the context of quantum protein folding, the objective is to predict the optimal configuration or conformation of a protein by determining the turns of all amino acids. It represents the minimum conformation energy, which is the most stable and favorable folded state of the protein. VQE is employed to find the optimal turn which has the minimum conformation energy. Note that the method of quantum protein folding is from the reference [1] and I just explain how to use quantum protein folding from [1]. I acknowledge the work and ideas of the reference [1] as it can help understand quantum protein folding.

Descriptive Image — Figure 1. The diamond lattice (a) sub-lattice A (b) sub-lattice B

Methodology

Denser encoding: The conformation of a protein is the relative orientations of the amino acids by determining the turns of all amino acids. Therefore, it is important to encode the turn by qubits. In the denser encoding, each turn between amino acids is represented by two qubits.

Representation of Turn Directions using Qubits

For the sub-lattice A:

00 : represents turn direction 0
01 : represents turn direction 1
10 : represents turn direction 2
11 : represents turn direction 3

For the sub-lattice B:

00 : represents turn direction \(\overline{0}\)
01 : represents turn direction \(\overline{1}\)
10 : represents turn direction \(\overline{2}\)
11 : represents turn direction \(\overline{3}\)

For a protein with N amino acids, there will be N-1 turns between adjacent amino acids. With the symmetry of the diamond lattice, the encoding of the first two turns as 01 and 00 is fixed. The total number of required qubits is 2*(N-3) as each turn is encoded on two qubits.

For example, a protein with N amino acids has a conformation with denser encoding as follows,

\[\underbrace{[01]}_{\text{turn 1 }} \underbrace{[00]}_{\text{turn 2}} \underbrace{[q_0 q_1]}_{\text{turn 3}} \cdots \underbrace{[q_{(2i-6)} q_{(2i-5)}]}_{\text{turn i}} \cdots \underbrace{[q_{(2N-8)} q_{(2N-7)}]}_{\text{turn N-1}}\]

With the assumption that the first turn is at the sub-lattice, and the subsequent turns alternate between sub-lattice A and B. We can have the following constraint:

- For odd turns, the turn occurs only at the sub-lattice A.

- For even turn, the turn occurs only at the sub-lattice B.

Turn indicator: It is used to ensure that one turn at the axis \(a \in \{0, 1, 2, 3\}\) on the sub-lattice A or \(\bar{a} \in \{\bar{0}, \bar{1}, \bar{2}, \bar{3} \}\) on the sub-lattice B is chosen. The turn indicator function is defined as \(f(q_i q_{i+1})\) = 1 if the turn is at the axis a \(\in \{0, 1, 2, 3\}\) or at the axis \(\bar{a} \in \{\bar{0}, \bar{1}, \bar{2}, \bar{3} \}\) otherwise 0. The turn indicator is quite important as all of the equations in the Hamiltonian is represented by it.

The turn indicator function on denser encoding at the turn i is given as follows,

\begin{align} f_0(i) &= (1-q_{(2i-6)})(1-q_{(2i-5)}) \\ f_1(i) &= (1-q_{(2i-6)})q_{(2i-5)} \\ f_2(i) &= q_{(2i-6)}(1-q_{(2i-5)}) \\ f_3(i) &= q_{(2i-6)}q_{(2i-5)} \\ \end{align}

Note that when i is odd, the turn occurs at the axis \(a \in \{0, 1, 2, 3\}\). When i is even, the turn occurs at the axis \(\bar{a} \in \{\bar{0}, \bar{1}, \bar{2}, \bar{3}\}\). In the following, I will use \(f_a(i)\) as a simpy representation but remember that the parity of i decides the turn at the axis a or \(\bar{a}\).

Hamiltonian: The objective is to find the optimal configuration which has the minimum conformation energy. The energy function Hamiltonian is given as follows:

\[H = H_{back} + H_{ch} + H_{in}\]

where \(H_{back}\) represents that protein folds back into itself, \(H_{ch}\) represents the position of residue satisfies chirality contraints, and \(H_{in}\) represents the interaction between amino acids.

Fold back constraint: it is not allowed residue to fold back into itself so the fold back constraint is added into the Hamiltonian. It means that two residues can not be at the same position in the tertiary structure.

Function T(i, j) is defined for each pair of residue i and j and returns 1 if and only if the turn i and j are at the same axis a or \(\bar{a}\).

\[T(i, j) = \sum_{a\in\{0, 1, 2, 3\}}f_{a}(i)f_{a}(j)\]

The fold back term is constructed as follows,

\[H_{back} = \sum_{i=3}^{N-1}\lambda_{back}T(i, i+1)\]

where \(\lambda_{back}\) is a penalty with larger positive that can be adjusted. When T(i, i+1) = 1, it means that two turns at the axis a and \(\bar{a}\) respectively are the same so the protein folds back into itself.

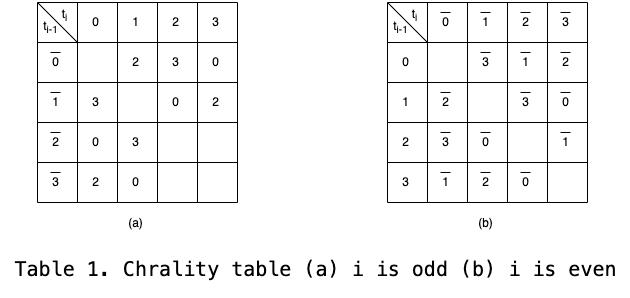
Chirality contraint: In proteins, the charality of amino acids plays a crucial role in determining the spatial arrangement of side chains relative to the main chain. The position of the side chain is influenced by the choice of the turn \(t_i \text{ and } t_{i+1}\). The chirality contraint is added to the Hamiltonian for ensuring the correct chirality. Here, I only consider the first side residue of the position bead i on the main chain. It is easy to list all of possible turns of the side chain as it can be determined by the main chain turn \(t_i \text{ and } t_{i+1}\).

The expected indicator of the first bead of side chain on the main chain i is constructed with the turn i-1 and i.

\begin{align} f_{0}^{exp}(i^{(1)}) &= (1-g_i)(f_1(i-1)f_2(i) + f_2(i-1)f_3(i) \\ &+ f_3(i-1)f_1(i)) + g_i(f_1(i-1)f_3(i) \\ &+ f_2(i-1)f_1(i) + f_3(i-1)f_2(i)) \end{align}

\[\begin{align} f_{1}^{exp}(i^{(1)}) &= (1-g_i)(f_0(i-1)f_3(i) + f_2(i-1)f_0(i) \\ &+ f_3(i-1)f_2(i)) + g_i(f_0(i-1)f_2(i) \\ &+ f_2(i-1)f_3(i) + f_3(i-1)f_0(i)) \end{align} \]

\[\begin{align} f_{2}^{exp}(i^{(1)}) &= (1-g_i)(f_0(i-1)f_1(i) + f_1(i-1)f_3(i) \\ &+ f_3(i-1)f_0(i)) + g_i(f_0(i-1)f_3(i) \\ &+ f_1(i-1)f_2(i) + f_3(i-1)f_1(i)) \end{align} \]

\[\begin{align} f_{3}^{exp}(i^{(1)}) &= (1-g_i)(f_0(i-1)f_2(i) + f_1(i-1)f_0(i) \\ &+ f_2(i-1)f_1(i)) + g_i(f_0(i-1)f_1(i) \\ &+ f_1(i-1)f_2(i) + f_2(i-1)f_0(i)) \end{align} \]

\[g_i = \frac{1 + (-1)^i}{2}\]

Where \(g_i\) is introduced for the parity of i. \(g_i\) is 0 when i is odd otherwise 1.

The chirality contraint is constructed according to the Table 1 where the structure is constraint when the expected turn and real turn is different.

\[H_{ch} = \lambda_{ch}\sum_a\sum_{i=2}^{N-1}(1-f_a(i^{(1)}))f_a^{exp}(i^{(1)})\]

Where \(\lambda_{ch}\) is a larger positive to penalty the incorrect structure on chirality. Note that the first and last amino acid on the main chain has no side chain.

Interaction: The interaction Hamiltonian represents interactions between amino acids.

\[H_{in} = H_{in}^{(1)} + H_{in}^{(2)} + H_{in}^{(3)} + \cdots\]

where \(H_{in}\) represents the total interaction. \(H^{(l)}\) represents the lth nearest neighbour interaction. \(H_{in}^{(1)}\) represents the first nearst neighbour interactions, \(H_{in}^{(2)}\) represents the second nearest neighbour interactions, and \(H_{in}^{(3)}\) represents the third nearest neighbour interactions. Here it involves the distance, so I need to introduce the distance concept before explaining the interaction Hamiltonian.

Distance: It represents relative location between amino acids. The distance between beads is defined as the number of turns along the main chain. \(n_{a}(i, j)\) is defined as the number of turns at the axis \(a \in \{0, 1, 2, 3\}\) and \(n_{\bar{a}}(i, j)\) is defined as the number of turns at the axis \(\bar{a} \in \{\bar{0}, \bar{1}, \bar{2}, \bar{3}\}\). We know that the turns at the sub-lattice A and B is alternated and the directions of the axis a and \(\bar{a}\) is antipodal. Therefore, we assume that the number of turns occurring at the axis a is positive while it is negative at the axis \(\bar{a}\). \(\Delta n_a(i, j) = n_a(i, j) - n_{\bar{a}}(i, j)\) is defined as the real distance between bead i and j at the axis a.

\[\Delta n_a(i, j) = \sum_{k=i}^{j-1}(-1)^{k+1}f_a(k)\]

Note that the turn is at the axis a when i is odd.

The distance between beads on the side chain \(i^{(s)}\) and \(j^{(p)}\) is defined as follows, where \(i^{(s)}\) represents the sth bead of the side chain at position i on the main chain, and \(j^{(p)}\) represents the pth bead of the side chain at the position j.

\[\Delta n_a(i^{(s)}, j^{(p)}) = \Delta n_a(i, j) + \sum_{l=1}^{p}(-1)^{j+l+1}f_a(j^{l}) - \sum_{l=1}^{s}(-1)^{i+l+1}f_a(i^{(l)})\]

x(i, j) is defined as follows,

\[x(i, j) = \begin{pmatrix} \Delta n_0(i, j) \\ \Delta n_1(i, j) \\ \Delta n_2(i, j) \\ \Delta n_3(i, j) \\ \end{pmatrix}\]

The actual distance is defined as d(i, j),

\[d(i, j) = \Vert x(i, j) \Vert_2^2 = \sum_{a} \Delta n_a(i, j)^2\]

First nearest neighbour interaction: \(H_{in}^{(1)}\) is the interaction between amino acids that are one distance apart and not directs with each other. We consider the beads i and j with j > i+2. For the one distance between beads, j - i = 1 mod 2.

\[H^{(1)} = \sum_{i=1}^{N-3}\sum_{\substack{j>i+2 \\ \text{j-i=1 mode 2}}}^{N} h_{i, j}^{(1)}\]

\[h_{i, j}^{(1)} = E_{i, j}^{(1)} + \lambda_1(d(i, j) - 1)\]

where \(E_{i, j}^{(1)}\) represents the interaction energy between beads i and j. Only the beads that have one distance can contribute to the interaction. The case of beads that have the distance with more than one can be added to a penalty with a larger positive.

Second nearest neighbour interaction: \(H_{in}^{(2)}\) is the interaction between amino aicds that are two distance.

\[H^{(2)} = \sum_{i=1}^{N-3}\sum_{\substack{j>i+2 \\ \text{j-i=0 mode 2}}}^{N} h_{i, j}^{(2)}\]

\[h_{i, j}^{(2)} = E_{i, j}^{(2)} + \lambda_1(d(i, j) - 2)\]

where \(E_{i, j}^{(2)}\) represents the interaction energy between beads i and j. Only the beads that have two distance can contribute to the interaction. The case of beads that have the distance with more than two can be added to a penalty with a larger positive.

Reference