It is the first quantum algorithm I begin the journey of exploring quantum algorithms. It is design to find a hidden bitstring and can be applied in crytography, function inversion, and database search.
Problem definition: given an oracle(black box) function f(x) where it runs the given a hidden bitstring with the length of n, how to find it?
\[ f(x) = s \cdot x \text{ (mod 2)} = (s_1x_1 + s_2x_2 + \cdots + s_nx_n) \text{ (mod 2)} \]
In classical computing, it requires n queries because each query can get only one single bit of the hidden bitstring. The algorithm has a time complexity of O(n).
In quantum computing, it only needs one query so the time complexity is O(1). This quantum algorithm has a speedup over classical one. It shows the power of quantum parrallelism in solving certain types of problems is more efficient than classical computing.
A useful representation of applying H gates on n qubits.
I take an example with applying two H gates on two qubits |0>|0>.
\[|0>|0> \xrightarrow{H \otimes H} \frac{|0>+|1>}{\sqrt{2}}\frac{|0>+|1>}{\sqrt{2}} = \frac{1}{2}(|00> + |01> + |10> + |11>) = \frac{1}{2}\sum_{x=0}^{3}|x>\]
Where x represents the binary string, such as 0 is 00, 1 is 01, 2 is 10, and 3 is 11. Note that x is a binary number in all the chapter and each bit represents one qubit. For example, when x = 01010, the first qubit is 0, second one is 1, ..., and the last one is 0. Reader will be confused when they do not know x as a binary number.
Following the method and then applying n H gates on n qubits.
\[|0>_n \xrightarrow{H^{\otimes n}} \frac{1}{\sqrt{2^n}} \sum_{x=0}^{2^n-1}|x>\]
When the input state is an arbitrary value |a>, what is the output of applying H gates on qubits.
Firstly, one qubit |a> is as an example,
\[H|a> = \begin{cases} \frac{|0>+|1>}{\sqrt{2}} \text{if a} = 0 \\ \frac{|0>-|1>}{\sqrt{2}} \text{if a} = 1 \end{cases} \]
Then,\[H|a> = \frac{1}{\sqrt{2}} (|0> + (-1)^a|1>) = \frac{1}{\sqrt{2}} \sum_{0}^{1}(-1)^{a \cdot x}|x>\]
Now we can apply H gates on an arbitrary |a> that has n qubits, where a is a binary number, a = \(a_0a_1 ... a_j ... a_{n-1}\)
\[ \begin{align} H^{\otimes n}|a> &= H|a_0> \otimes H|a_1> \otimes ... \otimes H|a_{n-1}> \\ &= \frac{1}{\sqrt{2}} \sum_{x_0=0}^{1}(-1)^{a_0 \cdot x_0}|x_0> \frac{1}{\sqrt{2}} \sum_{x_1=0}^{1}(-1)^{a_1 \cdot x_1}|x_1> ... \frac{1}{\sqrt{2}} \sum_{x_{n-1}=0}^{1}(-1)^{a_{n-1} \cdot x_{n-1}}|x_{n-1}> \\ &= \frac{1}{\sqrt{2^n}} \sum_{x_0=0}^{1}\sum_{x_1=0}^{1} ... \sum_{x_{n-1}=0}^{1}(-1)^{a_0 \cdot x_{0} + a_1 \cdot x_1 + ... + a_{n-1} \cdot x_{n-1}} |x_0>|x_1> ... |x_{n-1}> \\ &= \frac{1}{\sqrt{2^n}} \sum_{x=0}^{2^n-1}(-1)^{a\cdot x}|x> \end{align} \]
where \(a \cdot x\) represents the bitwise inter product of a and x.
A common Oracle
I will introduce the concept of quantum oracle in quantum computing again before talking about the BV algorithm. A quantum oracle is a block box with a combination of quantum gates that can complete a specific function. It is not important to know how to construct the oracle function with quantum circuits now. The circuits of an oracle are designed according to the specific function.
A common quantum oracle is as follows, where x represents data qubits and y represents target qubits. The outcome of x has no changes and the outcome of y is \(y \oplus f(x)\). I will take an example of an oracle when introducing the BV algorithm later.
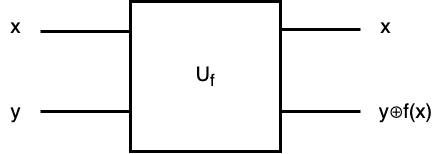
When x = \(\frac{|0>+|1>}{\sqrt{2}}\) and y = |1>, then the outcome is:
\[|x>|y\oplus f(x)> = \frac{|0>|1\oplus f(0)> + |1>|1\oplus f(1)>}{\sqrt{2}} = \frac{|0>|\overline{f(0)}> + |1>|\overline{f(1)}>}{\sqrt{2}}\]
How the BV algorithm can work.
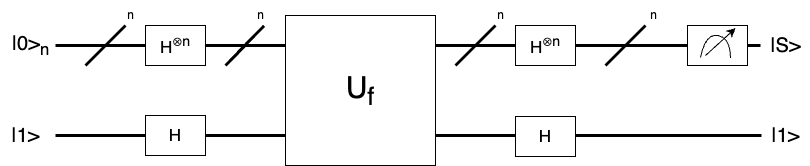
The circuit of BV algorithm consists of H gates and an oracle. The oracle is mentioned above. It seems quite easy.
The input states are n qubits in the state |0> and one qubit in the state |1>.
After act H gate on \(|0>_n\) and |1> respectively, the quantum state:
\[|\phi_1> = H^{\otimes n}|0>_n \otimes H|1> = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}|x> \otimes \frac{|0> - |1>} {\sqrt{2}}\]
The quantum state \(|\phi_1>\) goes through an oracle, then the quantum state:
\[\begin{align} |\phi_2> &= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} \frac{|x>|f(x)> - |x>|\overline{f(x)}>}{\sqrt{2}} \\ &= \begin{cases} \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} \frac{|x>|0> - |x>|1>}{\sqrt{2}} \text{if f(x)} = 0\\ \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} \frac{|x>|1> - |x>|0>}{\sqrt{2}} \text{if f(x)} = 1\\ \end{cases} \\ &= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} (-1)^{f(x)}|x>\frac{|0> - |1>}{\sqrt{2}} \end{align} \]
After act H gate on \(|\phi_2>\) again, the quantum state:
\[\begin{align} |\phi_3> &= H^{\otimes n}\frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} (-1)^{f(x)}|x> \otimes H\frac{|0> - |1>}{\sqrt{2}} \\ &= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}\frac{1}{\sqrt{2^n}}\sum_{y=0}^{2^n-1} (-1)^{f(x) + x\cdot y}|y> |1> \\ &= \frac{1}{2^n}\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1} (-1)^{f(x) + x\cdot y}|y> |1> \end{align} \]
We know \(f(x) = \sum_{j=0}^{n-1} s_j\cdot x_j\), then
\[\begin{align} |\phi_3> &= \frac{1}{2^n}\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1} (-1)^{\sum_{j=0}^{j=n-1}s_j\cdot x_j + \sum_{j=0}^{j=n-1}x_j\cdot y_j}|y> |1> \\ & = \frac{1}{2^n}\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1} (-1)^{\sum_{j=0}^{j=n-1} (s_j + y_j)\cdot x_j}|y> |1> \\ \end{align} \]
We also know the total number of coefficient equals 1, so \(\sum_{j=0}^{j=n-1} (s_j + y_j)\cdot x_j\) is even. We can get s equals y because x is arbitrary and s and y are above zero.
\[|\phi_3> = \frac{1}{2^n}\sum_{x=0}^{2^n-1} |s>|1> = |s>|1> \\\]
The outcome is s that is a binary string after measurement. It represents we can get the string after only one executes on a quantum computer.
The example of BV algorithm
I complete the BV algorithm on Qiskit. The s string is "10010". First, we need to construct an oracle that has the function f(x) = \(s \cdot x \) mod 2 with the s string. x is the input state. Only if one bit of s string equals 1, applying a CNOT gate on the last qubit. The outcome of qiskit is that the first qubit always locates the most right. I want to get outcome where the first locates the most left. I reverse the s string when constructing the oracle.

Result
We can see the outcome is "10010" which is equals the s string. This proofs that we complete the BV algorithm. Readers can use arbitrary binary string to test the BV algorithm. I do not know whether I clearly explain the algorithm. You can contact me when you have questions.