Quantum Search Algorithm, known as Grover's search algorithm, is to search unstructured data for finding the result with highest probability [1]. In classical computing, the time complexity of a common search algorithm is O(N). In quantum computing, the complexity of quantum search algorithm is \(O(\sqrt{N})\) which can achieve a quadratic speedup over classical ones.
I write down the process of the quantum search algorithm according to my idea. It may mislead readers and hope you can understand it. You can contact me and give me advice when you have questions. I will appreciate in advance.
Suppose we have unstructured data, the number of data is N and we require n = \(log(N)\) qubits. The target of Grover's search is to find the target x with the highest probability. We need to make sure that the x is different from other quantum states. One way is to repeatedly amplify amplitude of the x and decrease other quantum states. The x has the highest probability through several times repeat. At last, we can get the x through measurement.
The process of the Grover's algorithm includes encoding, constructing oracle, amplitude amplification, and repeat and measurement.
1. Encoding: convert data to quantum states
2. Oracle: construct an oracle \(U_\omega\), which can flip the sign of the amplitude of the solution states, otherwise the quantum states are unchanged.
\[ \begin{cases} U_\omega|x> = -|x> \text{ when x } = \omega\\ U_\omega|x> = |x> \text{ when x } \ne \omega\\ \end{cases} \]
3. Amplification: increase the probability amplitude of the solutions while decreasing
\[W = 2|\Phi><\Phi| - I\] where \(|\Phi> = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}|x>\)
4. Repeat: iteration the step 2 and step 3
All processes of Grover's search are combined and the structure of the Grover's search is as follows

Where V represents an oracle \(U_\omega\) and W represents amplification.
\[V = I - 2|\omega><\omega| \]
\[W = 2|\Phi><\Phi| - I \]
where \(|\Phi> = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}|x>\), and \(\omega\) is the target.
I will explain the process of Grover search one step by step. Before I illustrate the procedure, we need to know operations which can make the computation easy.
\[<\omega|\Phi> = \frac{1}{\sqrt{N}} \]
\[V|\omega> = (I - 2|\omega><\omega|)|\omega> = -|\omega>\]
\[W|\omega> = (2|\Phi><\Phi| - I)|\omega> = \frac{2}{\sqrt{N}}|\Phi> - |\omega>\]
\[V|\Phi> = (I - 2|\omega><\omega|)|\Phi> = |\Phi> - \frac{2}{\sqrt{N}}|\omega>\]
\[W|\Phi> = (2|\Phi><\Phi| - I)|\Phi> = |\Phi>\]
We can see the quantum circuit of Grover search. We set \(N = 2^n\), so n qubits are required. After acting n H gates on The input \(|0>^{\otimes n}\), the quantum states are
\[|\phi_1> = \frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x> = |\Phi>\]
After acting V on \(|\phi_1>\),
\[|\phi_2> = V|\Phi> = |\Phi> - \frac{2}{\sqrt{N}}|\omega>\]
After acting W on \(|\phi_2>\),
\[ \begin{align} |\phi_3> &= W|\phi_2> \\ &= W(|\Phi> - \frac{2}{\sqrt{N}}|\omega>) \\ &= |\Phi> - \frac{2}{\sqrt{N}}(\frac{2}{\sqrt{N}}|\Phi> - |\omega>) \\ &= (1 - \frac{4}{N})|\Phi> + \frac{2}{\sqrt{N}}|\omega> \end{align}\]
After iterations of oracle and amplification, the equation of quantum states of Grover becomes complex. So Grover's search is often explained using geometric intuition. Visualizing Grover's search as a rotation, we can understand how the repeated oracle and amplification amplify the probability of the solution state.
For convinience, a quantum state is provided,
\[|\Phi'> = \frac{1}{\sqrt{N-1}}\sum_{x\neq\omega}|x>\]
\[<\omega|\Phi'> = 0\]
It means that \(|\omega> \text{ and } \Phi'> \) has a 90 degree angle.
We can suppose the angle \(\theta\) between \(|\Phi> \text{ and } \Phi'>\),
\[\cos\theta = <\Phi|\Phi'> = \sqrt{\frac{N-1}{N}}\]
then \(\sin \theta = \frac{1}{\sqrt{N}} \text{ , } \theta \approx \frac{1}{\sqrt{N}}\) where N is large.
We can see the angle between \(|\Phi> \text{ and } |\phi_2>\),
\[<\Phi|\phi_2> = <\Phi|(|\Phi> - \frac{2}{\sqrt{N}}|\omega>) = 1 - \frac{2}{N} \]
\[\cos 2\theta = 1 - \frac{2}{N} \]
So the angle between \(|\Phi> \text{ and } |\phi_2>\) is \(2\theta\).
We also can get the angle between \(|\Phi> \text{ and } |\phi_3>\),
\[<\Phi|\Phi_3> = <\Phi|[(1-\frac{4}{N})|\Phi> + \frac{2}{\sqrt{N}}|\omega>] = 1 - \frac{2}{N}\]
The angle is also \(2\theta\).
But We need to be sure the angle between \(|\Phi_2> \text{ and } |\Phi_3>\),
\[\begin{align} <\Phi_2|\Phi_3> &= (<\Phi| - \frac{2}{\sqrt{N}}<\omega|)[(1-\frac{4}{N})|\Phi> + \frac{2}{\sqrt{N}}|\omega>] \\ &= 1 - \frac{8}{N} + \frac{8}{N^2} \\ &= \cos 4\theta \end{align} \]
However, \(|\Phi_2> \text{ and } |\Phi_3>\) are not the same quantum state and the angle between them is \(4\theta\), so the rotations between \(|\Phi_2> \text{ and }|\Phi>\), and \(|\Phi_3> \text{ and } |\Phi>\) are two directions. We can draw the relationship between \(|\Phi>, |\Phi'>, |\Phi_2>, |\Phi_3>\), where \(|\Phi_2> = V|\Phi>, |\Phi_3> = WV|\Phi>\),
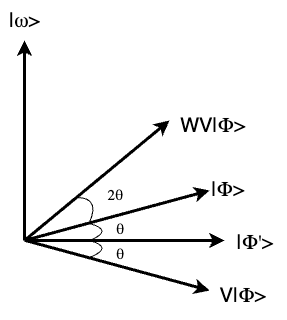
After t iterations of applying unitary W and V, the angle between the new quantum state \(|\Phi_t>\) and the target quantum state \(|\Phi>\) is \(2\theta t\). We want the new quantum state \(|\Phi_t>\) to be close to the target \(|\omega>\) so that we can find the target with the highest probability. Then we can have,
\[2\theta t = \frac{\pi}{2} - \theta\]
\[t = \frac{\pi}{4\theta} - \frac{1}{2} \approx \frac{\pi\sqrt{N}}{4} \approx \sqrt{N}\]
This means that we find the target after about \(\sqrt{N}\) iterations of applying the unitary W and V.
Example on Qiskit
The search solution space is {000, 001, 010, 011, 100, 101, 110, 111} and the targets are 011 and 110.
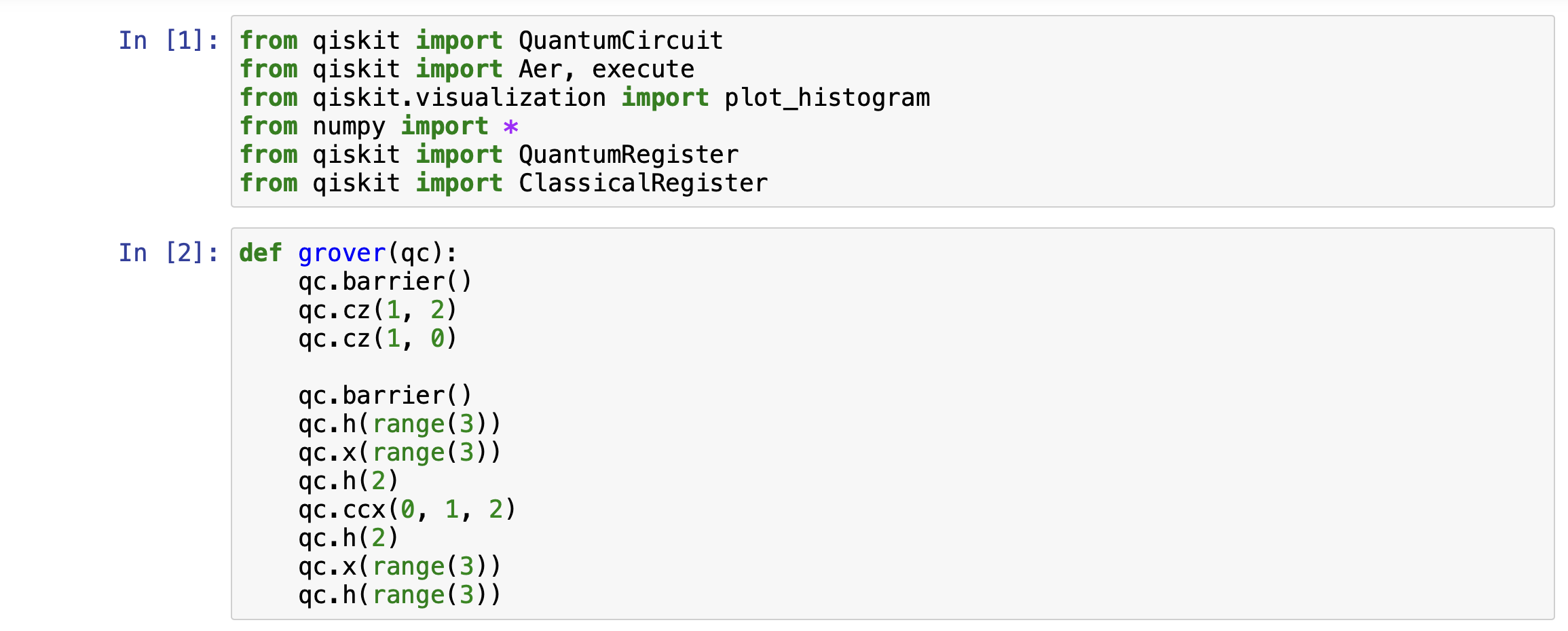
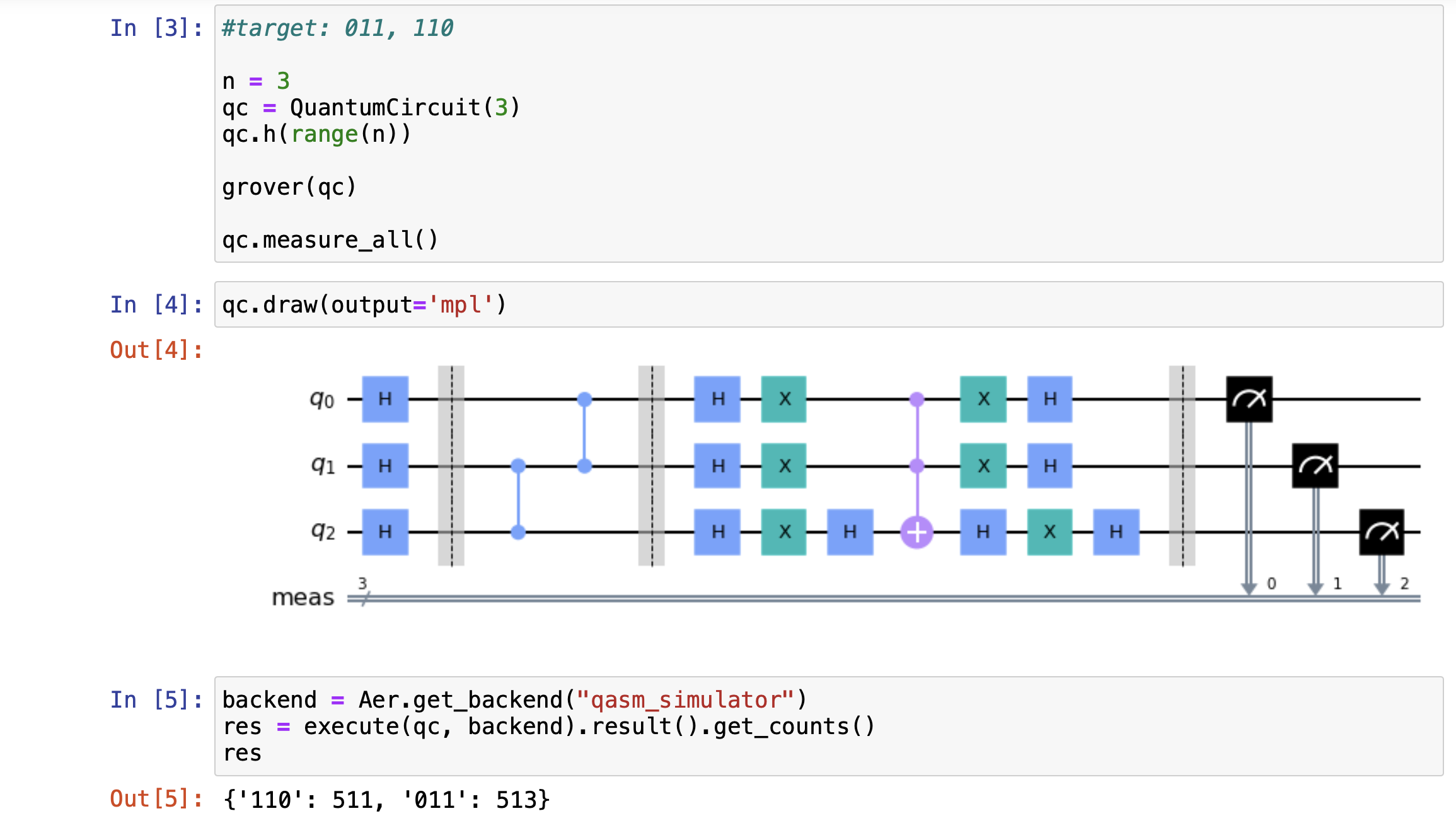
Result
We can see the result which includes 011 and 110 with the highest probabilities. It proves that we can get the target through Grover's search. Note that the Oracle will be designed according to the target.