Quantum phase estimation(QPE) is to estimate the phase of a given unitary operator. A unitary operator U with an eigenvector |u> and an eigenvalue \(e^{2\pi i\varphi}\) is known, but the value of \(\varphi\) is unknown. The target of QPE is to estimate \(\varphi\). For explaining the algorithm, we suppose an oracle which has a unitary operator U. The quantum circuit requires two registers, one is for the estimation of eigenvalue and the other is for the eigenstate. The number of qubits in the first register is decided by the accuracy we estimate for eigenvalue \(\varphi\). The first register begins in the state |0>. The second register begins in the eigenvector state |u>.
\[U|u> = e^{2\pi i\varphi}|u>\]
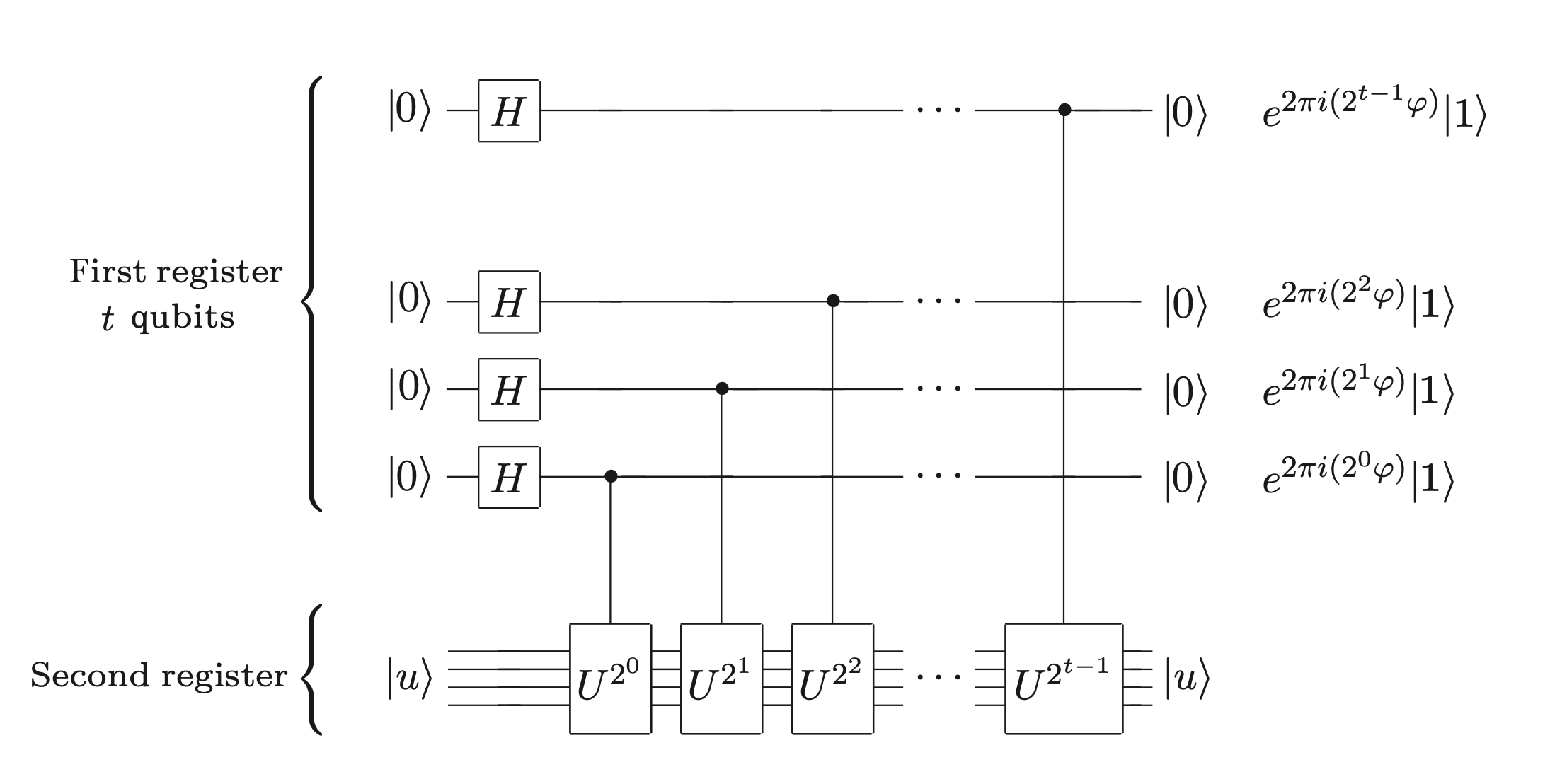
The quantum circuit above is applied, the outcome is
\[ \begin{align} |00\cdots 0>|u> &\xrightarrow{H^{\otimes t}} \frac{1}{\sqrt{2^t}}(|0>+|1>)(|0>+|1>)\cdots (|0>+|1>)|u> \\ &\xrightarrow{U^{2^0}} \frac{1}{\sqrt{2^t}}(|0>+|1>)(|0>+|1>)\cdots (|0>|u>+|1>U^{2^0}|u>) \\ &= \frac{1}{\sqrt{2^t}}(|0>+|1>)(|0>+|1>)\cdots (|0> + e^{2\pi i(2^0\varphi)}|1>)|u> \\ &\xrightarrow{U^{2^1}, \cdots, U^{2^t}} \frac{1}{\sqrt{2^t}}(|0>+e^{2\pi i(2^{t-1}\varphi)}|1>)(|0>+e^{2\pi i(2^{t-2}\varphi)}|1>)\cdots (|0> + e^{2\pi i(2^0\varphi)}|1>)|u> \\ \end{align} \]
Now we set \(\varphi\) can be represented in t bits, so \(\varphi = 0.\varphi_1\varphi_2 \cdots \varphi_t\). Only the binary representation of eigenvalue with the length of t can be obtained through QPE. This is the reason why the algorithm is called quantum phase estimation.
\[e^{2\pi i 2^l \varphi} = e^{2\pi i 2^l 0.\varphi_1\varphi_2 \cdots \varphi_l \cdots \varphi_t} = e^{2\pi i 2^l 0.\varphi_{l+1} \cdots \varphi_t}\]
\[\begin{align} &\frac{1}{\sqrt{2^t}}(|0>+e^{2\pi i(2^{t-1}\varphi)}|1>)(|0>+e^{2\pi i(2^{t-2}\varphi)}|1>)\cdots (|0> + e^{2\pi i(2^0\varphi)}|1>)|u> \\ =& \frac{1}{\sqrt{2^t}}(|0>+e^{2\pi i(0.\varphi_t)}|1>)(|0>+e^{2\pi i(0.\varphi_{t-1}\varphi_{t})}|1>)\cdots (|0> + e^{2\pi i(0.\varphi_t)}|1>)|u> \\ \end{align} \]
It is easy to see the quantum state is the outcome of QFT on \(|\varphi>\). After applying IQFT on the quantum state, we can get the eigenvalue \(|\varphi>\). The quantum circuit of QPE as follows,
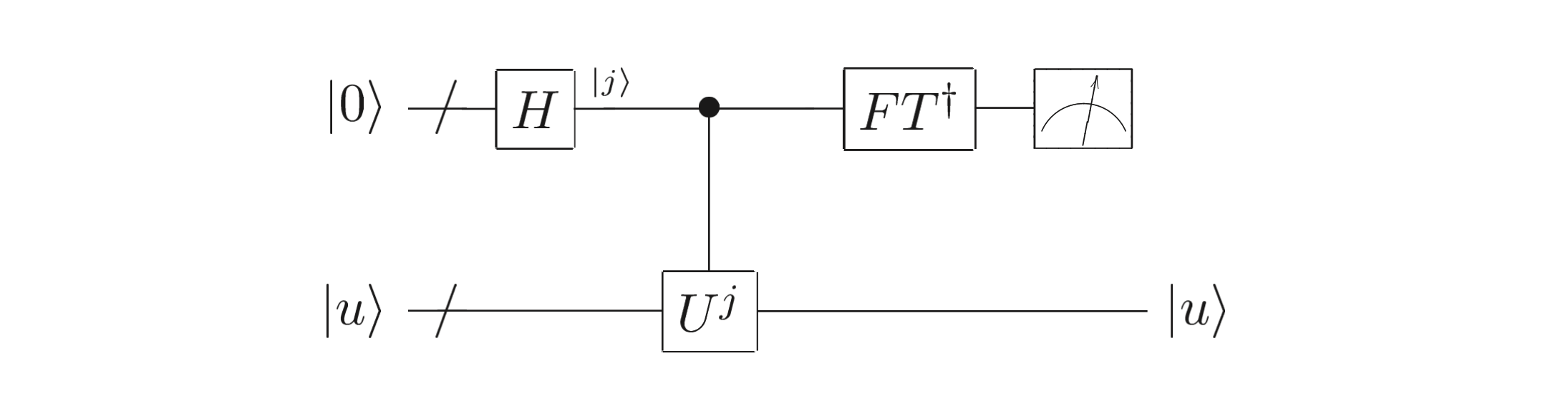
Where the first register contains t qubits, the second register is an eigenstate of a unitary U. We can see that the core of QPE is how to prepare the second register and the unitary operator U.
Example on Qiskit
I give an easy example of QPE to explain how it can be executed on Qiskit. The unitary operator U as follows,
\[ U = \begin{pmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{4}} \end{pmatrix} \]
One eigenvector of U is [0, 1] with the eigenvalue \(e^{\frac{i\pi}{4}}\). We can prepare the second register with |1> and the unitary operate is T gate.
\[U|1> = e^{2i\pi \varphi}|1> = e^{\frac{i\pi}{4}}|1>\]
so we expect to get \(\varphi = \frac{1}{8}\).



Result
The final outcome is |001> with the probability of 100%. We know \(\varphi = 0.\varphi_0\varphi_1\varphi_2 \text{ where } \varphi_0 = 0, \varphi_1 = 0, \varphi_2 = 1 \). The final eigen value is \(\frac{1}{8}\), which is the same as the actual value.