Shor's Algorithm is used to find the prime factors of an composite integer. It utilizes both quantum and classical components to achieve this task efficiently. Suppose we want to factorize a composite integer N. The process is as follows
1. Classical part: Select a random integer a and gcd(a, N) where 1< a < N
2. Quantum part(Period Finding): construct a quantum circuit to find the period r of the function \(f(x) = a^x\) mod N. If r is odd, we repeat the step 1 and 2 until r is even.
3. Classical part: use the period r to find the factors of N with classical algorithm.
I give an example with N = 21.
1. We select a = 5 as gcd(5, 21) = 1
2. We use quantum algorithm to find the period r of the function f(x) = \(5^x\) mod 21.
\[\begin{align} 5^1 \text{ mod } 21 &= 5 \\ 5^2 \text{ mod } 21 &= 4 \\ 5^3 \text{ mod } 21 &= 20 \\ 5^4 \text{ mod } 21 &= 16 \\ 5^5 \text{ mod } 21 &= 1 \\ \end{align} \]
So we can get the period r = 5. We select a = 2 again because 5 is odd.
\[\begin{align} 2^1 \text{ mod } 21 &= 2 \\ 2^2 \text{ mod } 21 &= 4 \\ 2^3 \text{ mod } 21 &= 8 \\ 2^4 \text{ mod } 21 &= 16 \\ 2^5 \text{ mod } 21 &= 11 \\ 2^6 \text{ mod } 21 &= 1 \\ \end{align} \]
The period r is 6. Then we can use classical method to find the factor of N.
3. We set \(x = a^{\frac{r}{2}} = 2^3 = 8\).
gcd(x-1, 21) = gcd(7, 21) = 7
gcd(x+1, 21) = gcd(9, 21) = 3
So, the factor of N are 7 and 3.
4. We can verify 3 * 7 = 21. This proofs that the algorithm can find the factor of a composite integer.
I can not give the proof of the algorithm and only the procedure is given.
\[\begin{align} a^r &= 1 \text{ mod N }\\ (a^{\frac{r}{2}} + 1)(a^{\frac{r}{2}} - 1) &= 0 \text{ mod N } = kN \text{ where }k = 0, 1, 2, \cdots\\ \end{align} \]
This is why we require the period r is even. Then set x = \(a^{\frac{r}{2}}\), and x + 1 and x -1 have greatest common divisor with N respectively. The gcd(x+1, N) and gcd(x-1, N) are used to find the factors of N. These gcd provide potential factors of N, which can be verified using classical methods.
Quantum part
I focus on how to use quantum algorithm to find the period r of the function f(x) = \(a^x\) mod N. This is called order-finding. Finding the period r is equal to find the least integer r (r>0), \(a^r \text{ mod N } = 1\). I will introduce how to construct quantum circuits for order-finding. It includes two registers, one is to store the phase estimation of a unitary and the other is to a unitary operator.
The unitary operator of Shor is an Oracle which can complete a specific function, like
\[U|y> = |xy \text{ mod } N>\]
The Shor's algorithm leverages the phase estimation to obtain the period r. We need to know the eigenstate of the unitary. We choose one eigenstate,
\[|u_s> = \frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}e^{-\frac{2\pi isk}{r}}|x^{k} \text{ mod N}>\]
where \(0 \leq s \leq r-1\), we can get a group of eigenstate.
After applying a unitary U, set \(\omega = e^{\frac{2\pi is}{r}}\)
\[\begin{align} U|u_s> &= \frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}e^{-\frac{2\pi isk}{r}}U|x^{k} \text{ mod N}> \\ &= \frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}e^{-\frac{2\pi isk}{r}}|x^{k+1} \text{ mod N}> \\ &= \frac{1}{\sqrt{r}}(|x> + e^{-\frac{2\pi is}{r}}|x^2> + \cdots + e^{-\frac{2\pi is(r-1)}{r}}|x^r>) \\ &= \omega\frac{1}{\sqrt{r}}(e^{-\frac{2\pi is}{r}}|x> + e^{-\frac{2\pi i2s}{r}}|x^2> + \cdots + e^{-\frac{2\pi isr}{r}}|1>) \\ &= \frac{\omega}{\sqrt{r}}\sum_{k=0}^{r-1}|x^k> \\ &= \omega|u_s> \end{align}\]
Where I ignore mod N in all \(|x^k>\). \(e^{\frac{2\pi is}{r}}\) is the eigenvalue of the eigenstate \(|u_s>\). We can apply the phase estimation on the eigenstate to get the phase \(\frac{s}{r}\). However, we need to note it is difficult to construct the eigenstate \(|u_s>\) because we do not know the s and r which we want to obtain.
An observation is useful to solve the problem of preparing \(|u_s>\),
\[\begin{align} \frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}|u_s> &= \frac{1}{r}\sum_{s=0}^{r-1}\sum_{k=0}^{r-1}e^{-\frac{2\pi isk}{r}}|x^k> \\ &= \frac{1}{r}\sum_{k=0}^{r-1}\sum_{s=0}^{r-1}e^{-\frac{2\pi isk}{r}}|x^k> \\ &= \frac{1}{r}(\sum_{s=0}^{r-1}|1> + \sum_{k=1}^{r-1}\sum_{s=0}^{r-1}e^{-\frac{2\pi isk}{r}}|x^k>) \\ &= \frac{1}{r}(\sum_{s=0}^{r-1}|1> + \sum_{k=1}^{r-1}(\frac{1 - e^{-\frac{2\pi ikr}{r}}}{1 - e^{-\frac{2\pi ik}{r}}})|x^k>) \\ &= |1> \end{align} \]
Note that |1> is a binary representation. For example, when we choose 3 qubits on the second register for the eigenstate, the |1> equals |001>. This simplifies the preparation the eigenstates for the unitary. We know each eigenstate has the same phase of eigenvalue. Therefore, the phase s/r can be obtained through the phase estimation when the input of the second register is |1>. It is not enough to obtain the period r because we only get the estimation s/r. Classical methods are required to obtain r through the estimation of s/r. It is called the continued fraction expansion.
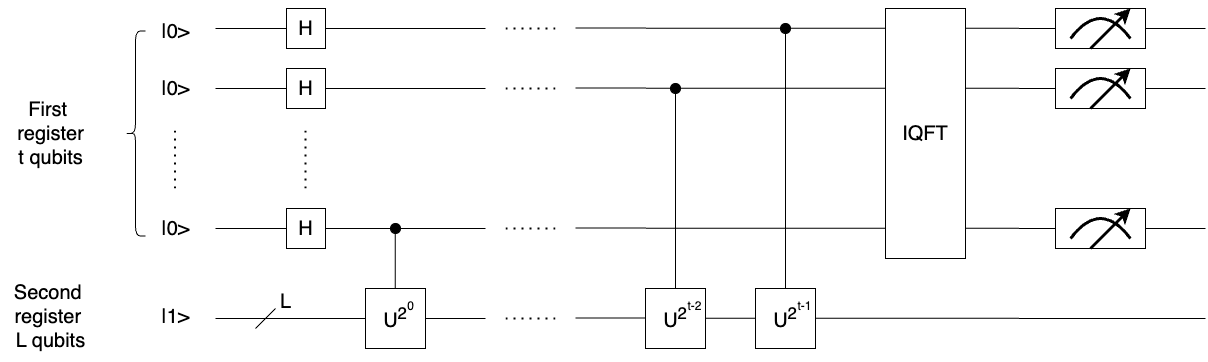
where L = \(\lceil log(N) \rceil\), and t = \(2L + 1 + \lceil log(2 + \frac{1}{2\varepsilon}) \rceil\)
Continued fraction expansion
Continued fraction expansion is used to represent a rational number as a sequence of integers, which can provide an approximation in terms of fractions. It satisfies our requirements, finding a fraction s/r that approximates the phase estimation \(\varphi\). The expression of the continued fraction is as follows,
\[ [a_0, a_1, \cdots, a_{n}] = a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{\cdots + \frac{1}{a_n}}}} \]
where \(a_0, a_1, \cdots, a_n \geq 0\). We defined the jth convergent when choose \([a_0, a_1, \cdots, a_j]\) where \(0 \leq j \leq\) n.
For instance, a rational number s/r where s and r are integers with r > 0 and s > 0.
1. Start with the integer part: \(\frac{s}{r}\) = integer part + fractional part.
2. Take the reciprocal of the fractional part.
3. Repeat this process until the fractional part becomes zeros or until you reach the convergent level you desire.
For example, we find the continued fraction expansion of a number 2.71828,
\[\begin{align} &2.71828 = 2 + \frac{1}{\frac{1}{0.71828}} = 2 + \frac{1}{1.39221}\\ &1.39221 = 1 + \frac{1}{\frac{1}{0.39221}} = 1 + \frac{1}{2.54965} \\ &2.54965 = 2 + \frac{1}{\frac{1}{0.54965}} = 1 + \frac{1}{1.81934} \\ &1.81934 = 1 + \frac{1}{\frac{1}{0.81934}} = 1 + \frac{1}{1.22049} \\ &\cdots \end{align} \]
We can obtain the continued fraction expansion:
2.71828 \(\approx [2, 1, 2, 1, \cdots ]\).
When we just chose [2, 1, 2, 1], then
\[2.71828 \approx 2 + \frac{1}{1 + \frac{1}{2 + \frac{1}{1}}} = \frac{11}{4}\]
Example on Qiskit
I give an example of Shor's algorithm on Qiskit. I refer the blog[3] that explains the shor's algorithm and has codes on Qiskit. The example factorizes the number 15.
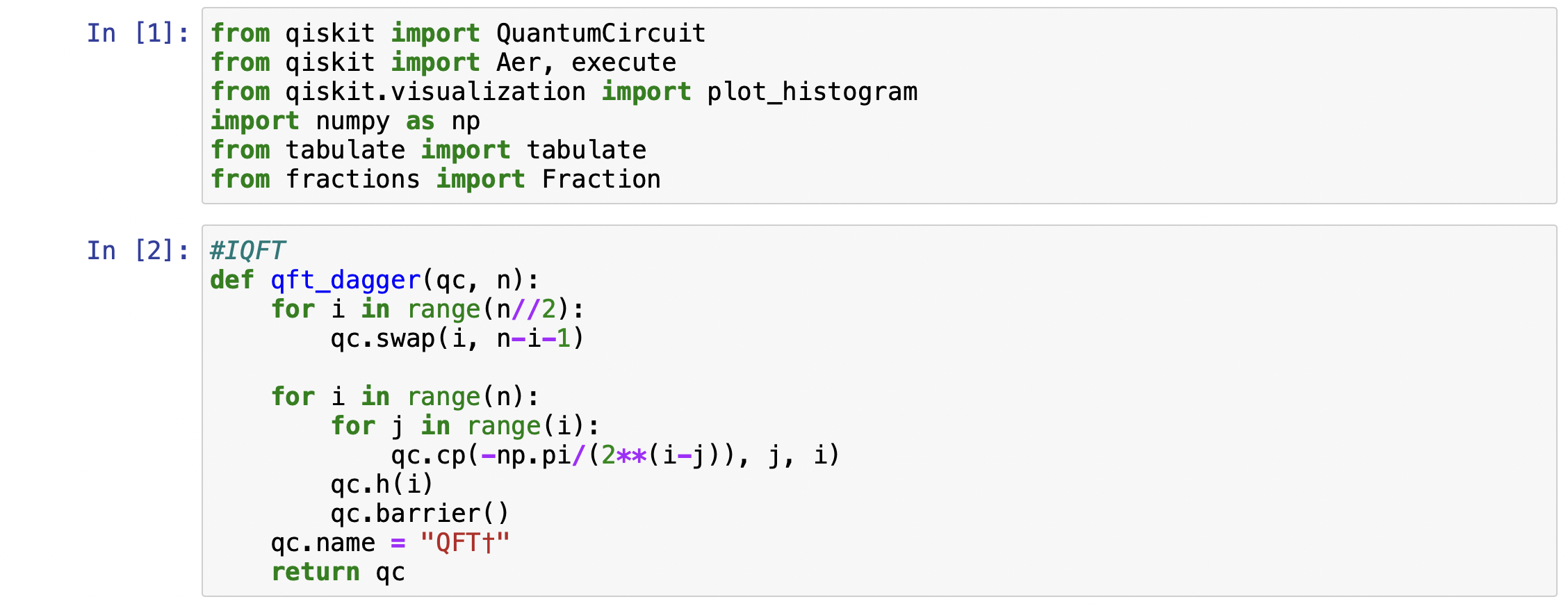

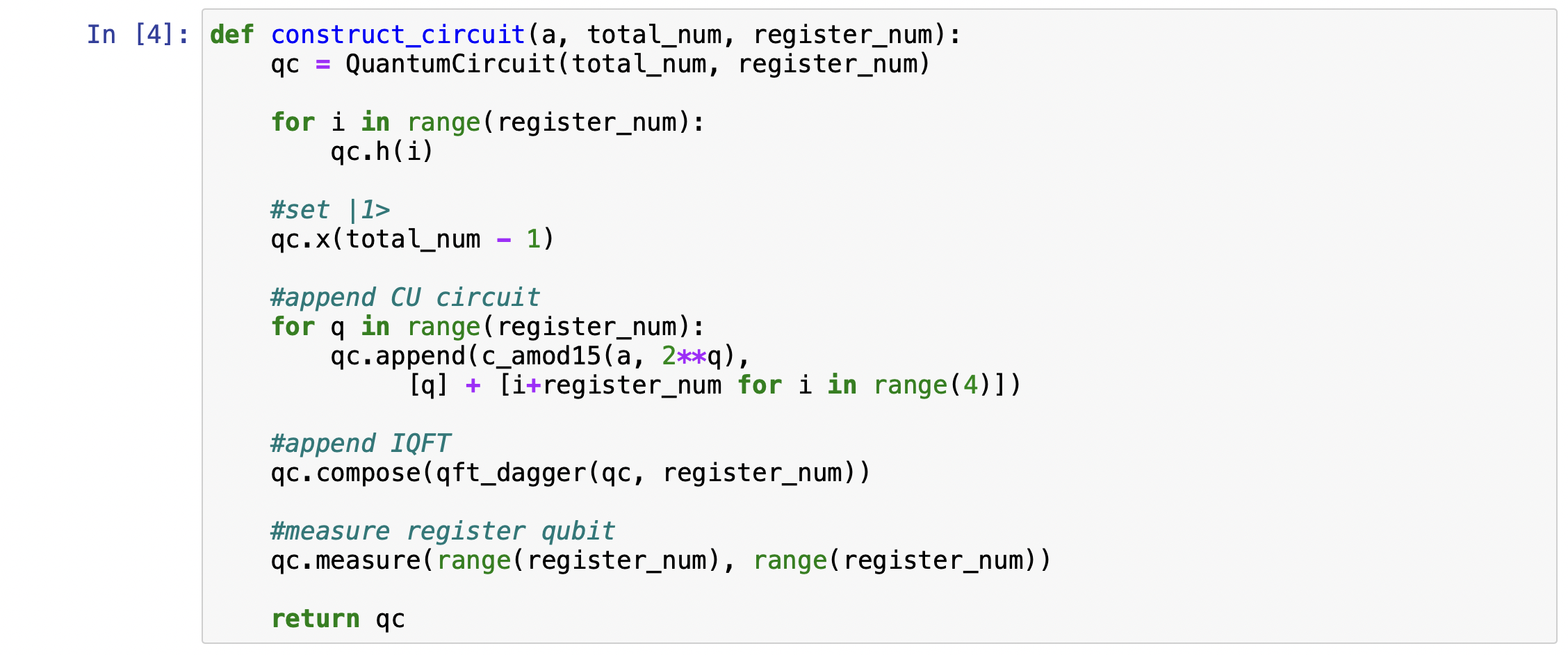

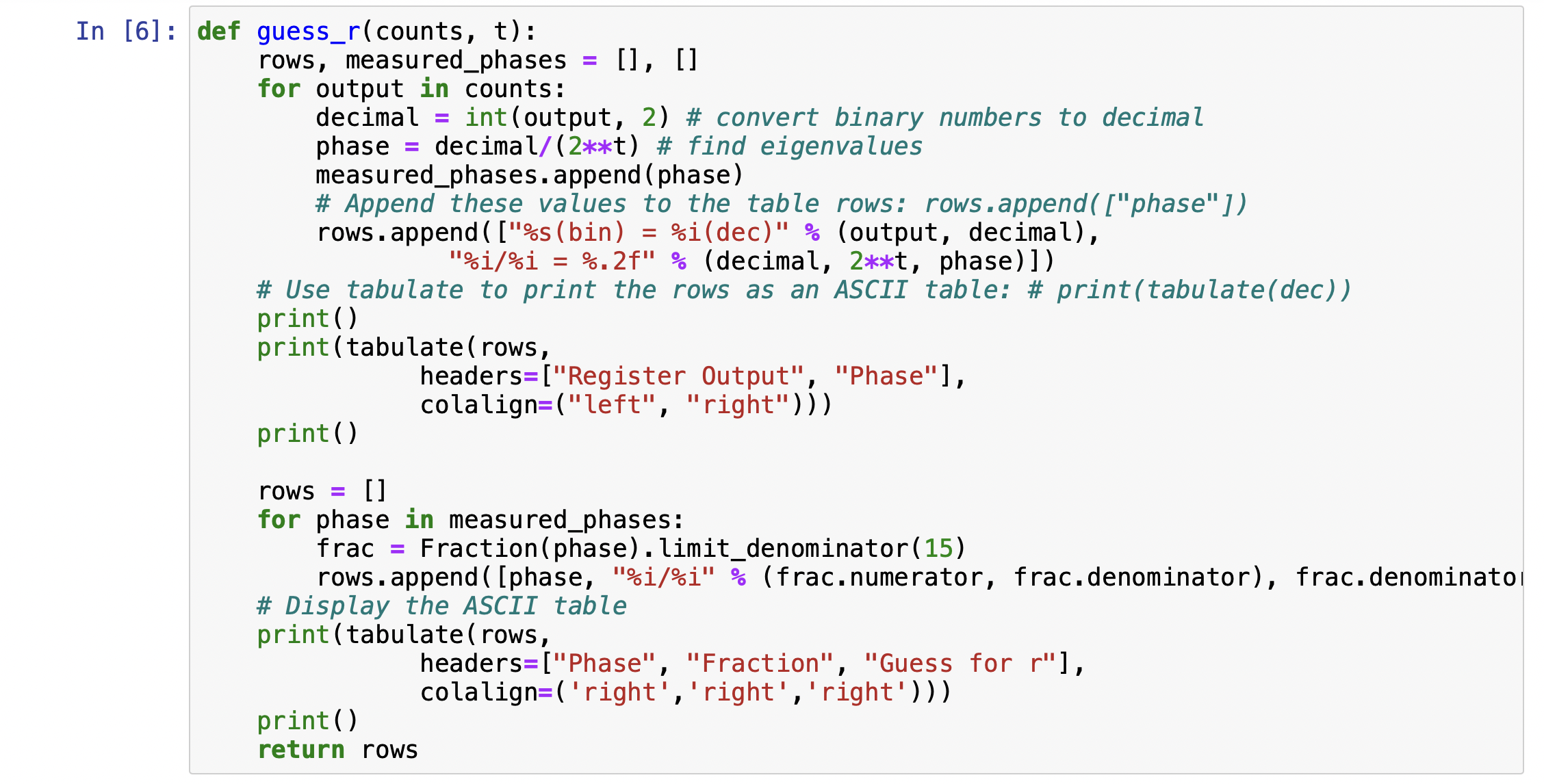


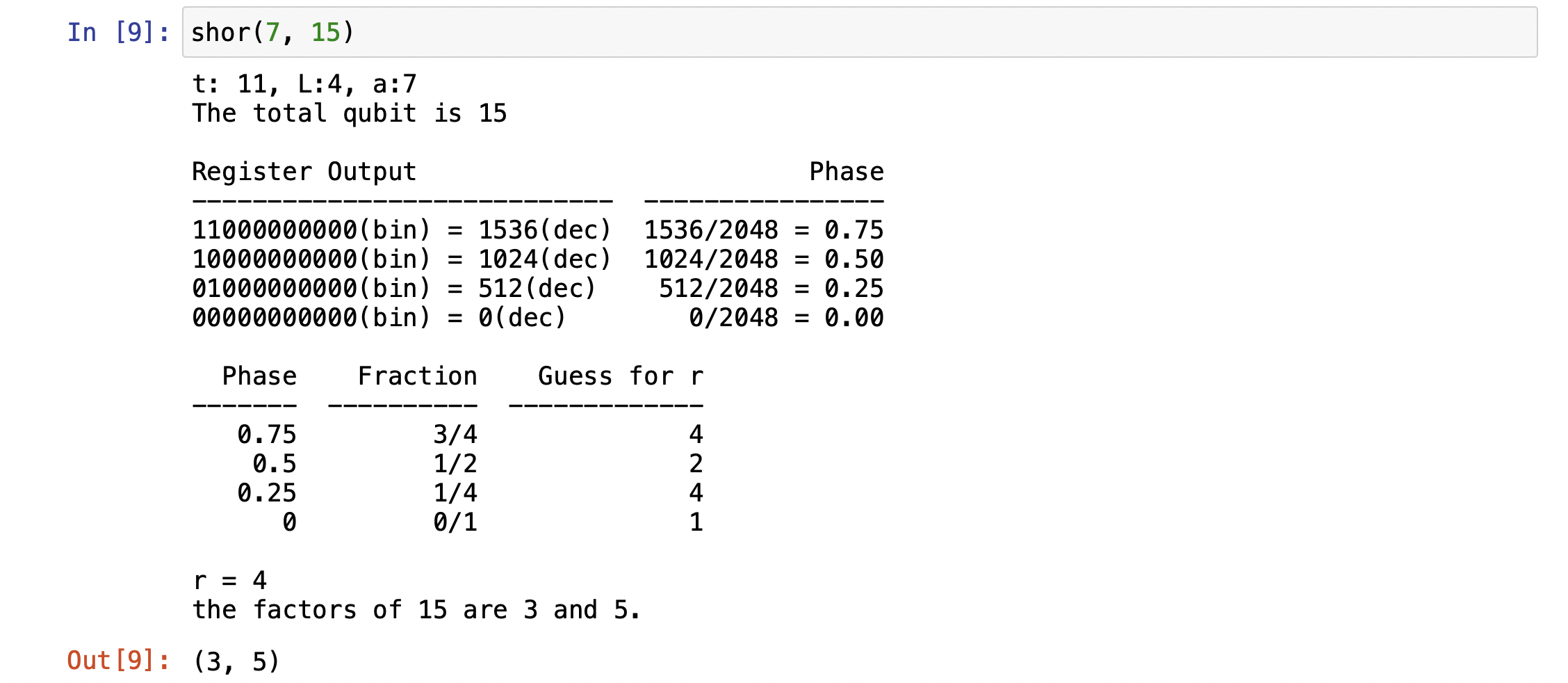
Result
In the example, 15 is factorized to 3 and 5. The result is what I expect.