What is a quantum circuit?
A quantum circuit is a computation model that utilizes a series of quantum gates to perform quantum operations on qubits. Quantum gates manipulate the quantum state of input qubits, producing a final state that represents the result of the computation. Due to the probability, multiple measurements of the quantum state are required to obtain final results.
Probabilistic outcomes: Unlike classical computing where the output is deterministic, the result of a quantum circuit are undeterministic. This means that executing the same quantum circuit multiple times might yield different results, and statistic analysis is used to interpret the final outcome.
Reversibility: One of the fundamental properties of quantum circuits is the reversibility. This stems from the fact that each quantum gate is a unitary operator, meaning the input state can be reconstructed from the output state by applying the appropriate inverse unitary gate. The unitary nature guarantees that the evolution of quantum states can be traced both forward and backward.
Superposition and entanglement: Unlike classical bits where can be either 0 or 1, qubits can exist in a superposition of both states |0> and |1>. This property, along with entanglement enables quantum circuits to perform complex computations that classical circuits can not be achieved.
Compare to classical circuits
For individuals with a background in classical digital circuits, understanding quantum circuits can be intuitive, as both types of circuits involve processing information from the input to output through gates. However, key differences lies in the quantum properties of superposition and entanglement, which allow qubits to exist in multiple states at once and interact in ways that classical bits can not. This lead to the potential for quantum circuits to perform certain computations much more efficiently that their classical counterparts.
There are comparasion between classical and quantum circuits.
1. Basic circuit composition:
Classical digital circuits: AND, OR, NOT, and XOR gates that perform classical Boolean operations on bits.
Quantum circuits: X, Y, Z, CNOT gates, etc, that acts quantum bits.
2. Flow of Circuits:
Classical digital circuits: information flows through the circuit via classical bits, which are always in a definite state of either 0 or 1. The flow of data is deterministic.
Quantum circuits: information is carried by qubits, which can exist in a superposition of states. The flow of information is governed by quantum principles, allowing for probabilistic operations.
3. Mathematical Model:
Classical digital circuits: Operations are described using boolean algebra, which deals with binary values and logical operations. Computation is based on manipulating bits using well-defined rules
Quantum circuits: quantum states are represented by unitary vectors, and quantum gates are described by unitary matrix. Linear algebra is the mathematical framework used to model the behaviour of quantum circuits, including operations like superposition and entanglement.
4. Superposition:
Classical digital circuits: process one bit at one time, which each bit having a distinct value of either 0 or 1 at any given moment.
Quantum circuits: allow for the parallel manipulation of multiple quantum states because of the principles of superposition and entanglement. A qubit can represent multiple states, enabling quantum circuits to perform calculations at once, leading to potential speedups in certain computations.
3.3.1 A quantum circuit example
In quantum circuits, the progression of computation typically unfolds from left to right, with quantum gates acting on qubit at each step. This is similar to classical circuits, where logical gates manipulates bits sequentially from input to output.
Explore the flow of quantum circuits using a simple quantum circuit from the book, "Classical and Quantum Information Theory: An Introduction for the Telecom Scientist"[1], This example illustrates how quantum circuits operate on qubits.
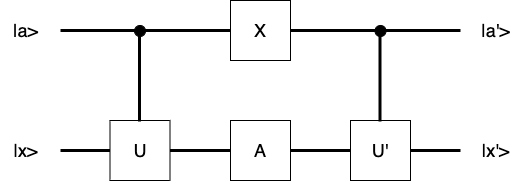
Consider the quantum circuit where the state |a> acts as a control qubit, and |x> is another qubit depending on |a>. The circuit uses various quantum gates to produce a final state from the input state. To clarify the process of the quantum circuits, we use two specific states and one common state to obtain the final state.
Case 1: When |a> = |0>,
1. Initial State:
\[|0>|x>\]
2. After applying CU gate:
\[ |0>|x> \xrightarrow{CU} |0>|x> \]
3. After X gate acts on the first qubit and A gate acts on the second qubit:
\[ |0>|x> \xrightarrow{XA} X|0>A|x> = |1>A|x> \]
4. After applying CU' gate:
\[ |1>A|x> \xrightarrow{CU'} |1>U'A|x> \]
Thus, the final state is:
\[ |1>U'A|x> \]
Case 2: When |a> = |1>,
1. Initial State:
\[|1>|x>\]
2. After applying CU gate:
\[ |1>|x> \xrightarrow{CU} |1>U|x> \]
3. After X gate acts on the first qubit and A gate acts on the second qubit:
\[ |1>U|x> \xrightarrow{XA} X|1>AU|x> = |0>AU|x> \]
4. After applying CU' gate:
\[ |0>AU|x> \xrightarrow{CU'} |0>AU|x> \]
Thus, the final state is:
\[ |0>AU|x> \]
Case 3: When |a> = \(\alpha|0> + \beta|1>\),
1. Initial State:
\[(\alpha|0> + \beta|1>)|x>\]
Thus, the final state is:
\[\alpha|1>U'A|x> + \beta|0>AU|x>\]