Two-qubit Gate
A two-qubit gate is a quantum gate that operates on two qubits simultaneously, introducing quantum entanglement or correlations between them. Two-qubit gates are critical for creating interactions between qubits, which are essential for the functioning of quantum algorithms and quantum circuits.
The common two-qubit gates include CNOT Gate, Controlled-U Gate, SWAP Gate.
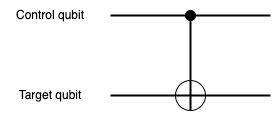
CNOT gate: the controlled-NOT gate assigns one qubit as the role of control qubit and pairs it with another as the target qubit. The target qubit flips its state when the control qubit is in the state |1>, and remain unchanged when the control qubit is in the state |0>. In classical computing, XOR operation performs a similar function. However, the CNOT gate introduces the superposition and entanglement of quantum mechanics. Unlike classical XOR, the CNOT gate allows qubits to exist in a superposition, representing multiple states simultaneously. The CNOT gate enables entanglement, a fundamental feature of quantum mechanics that allows qubit to be correlated in ways that support quantum parallelism and complex computation.
The matrix representation of CNOT gate:
\[CNOT = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}\]
CNOT gate operation on the computational basis states
CNOT|00> = |00>
CNOT|01> = |01>
CNOT|10> = |11>
CNOT|11> = |10>
The CNOT gate operates the general two-qubit input qubit \(|\psi>\)
\[|\psi>=\alpha_{00}|00> + \alpha_{01}|01> + \alpha_{10}|10> + \alpha_{11}|11>\]
After applying the CNOT gate to the input qubit \(|\psi>\),
\[ \begin{align} |\psi'> &= CNOT(\alpha_{00}|00> + \alpha_{01}|01> + \alpha_{10}|10> + \alpha_{11}|11>) \\ &=\alpha_{00}|00> + \alpha_{01}|01> + \alpha_{10}|11> + \alpha_{11}|10> \end{align} \]
Thus, the output state \(|\psi'>\),
\[|\psi'> =\alpha_{00}|00> + \alpha_{01}|01> + \alpha_{11}|10> + \alpha_{10}|11> \]
SWAP Gate
SWAP gate: swap the quantum state of two qubits. If the first qubit is in the state |a> and the second qubit is in the state |b>, after applying the SWAP gate, the first qubit is in the state |b> and the second qubit is in the state |a>.

The matrix representation of SWAP gate:
\[SWAP = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}\]
SWAP gate operation on the computational basis state
SWAP|00>=|00>
SWAP|01>=|10>
SWAP|10>=|01>
SWAP|11>=|11>
The SWAP gate operates the general two-qubit input qubit \(|\psi>\)
\[|\psi>=\alpha_{00}|00> + \alpha_{01}|01> + \alpha_{10}|10> + \alpha_{11}|11>\]
After applying the SWAP gate to the input qubit \(|\psi>\),
\[ \begin{align} |\psi'> &= SWAP(\alpha_{00}|00> + \alpha_{01}|01> + \alpha_{10}|10> + \alpha_{11}|11>) \\ &=\alpha_{00}|00> + \alpha_{01}|10> + \alpha_{10}|01> + \alpha_{11}|11> \end{align} \]
Thus, the output state \(|\psi'>\),
\[|\psi'> =\alpha_{00}|00> + \alpha_{10}|01> + \alpha_{01}|10> + \alpha_{11}|11> \]
SWAP gate can be decomposed into three CNOT gate. This is useful in quantum circuit design, as it allows to be implemented using a series of simpler operations.
The SWAP gate can be expressed as a sequence of three CNOT gates:
\[SWAP = CNOT_{01} \times CNOT_{10} \times CNOT_{01}\]
